Automatic timetable conflict resolution with genetic algorithms

Railway operations are underpinned by a valid, conflict-free timetable to which, thankfully, no major changes are made from day-to-day. However, changes and adjustments are a normal part of everyday operations and must be implemented in such a way that the timetable remains feasible. The reasons for making changes include scheduled deviations due to building measures or additional train paths.

When it comes to rescheduling the timetable, planners are currently reliant on the most powerful calculator known to the modern world – their brains. Rescheduling the timetable for a specific area requires a lot of experience given the many potential valid timetables there are to choose from. Timetable planners are responsible for finding a good solution; in other words, for defining a feasible timetable while keeping additional problems such as delays to a minimum. The aim is to revert to the standard timetable as quickly as possible following a line interruption. However, timetable planners cannot guarantee that their chosen timetable is the best of all potential solutions in the event of a disruption. The Infrastructure IT Solution Centre at SBB has therefore developed a fully automatic application to help timetable planners calculate a feasible, valid timetable at the push of a button in the event of disruptions or track/resource allocation conflicts.

Genetic algorithms as a solution to the problem

The use of conventional methods and algorithms did not seem a viable approach to solving this planning problem, since it is a so-called NP (nondeterministic polynomial) problem. In other words, the size of the search space in which planners look for a solution does not increase polynomially, but exponentially with the number of input parameters. By way of illustration, Figure 1 shows the potential options when two trains are travelling from A to B; once on a single-track and once with a passing track.

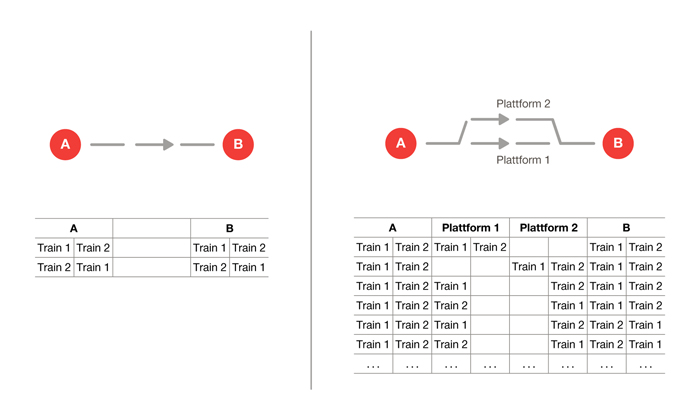
Figure 1: Diagram of options with single- and double-track lines

Simply adding a passing track expands the solution space from two to 12 valid options. The diagram shows that ‘Train 1’ always travels before ‘Train 2’ and consequently the number of options doubles again because Train 2 could equally travel before Train 1. It is important to note that these examples do not take timings into account. If the timings vary when the departure times and journey times change, this gives rise to a practically infinite problem space (search space).

In order to solve this complex problem, we draw on a method from the field of artificial intelligence – the ‘genetic algorithm’. This method follows the ‘survival of the fittest’ evolution strategy. Its strength lies in the fact that it converges even in very large problem spaces and finds good solutions, provided it is correctly parameterised. Each solution found guarantees that the timetable is feasible and conflict-free. However, further criteria such as punctuality and connecting services, which are used to evaluate the quality of the timetable, come into play in everyday operations. These soft criteria enable each of the timetables found to be re-evaluated in terms of the current state of operations. However, they are also difficult to integrate into the algorithm and so it cannot be guaranteed that any one option represents the best solution when measured against these soft criteria. The likelihood of the algorithm finding the best solution is inversely proportional to the complexity of the problem to be solved.

Ultimately it is more important to find a good solution quickly than to find the perfect solution, at too late a stage.

How the genetic algorithm works

The genetic algorithm is set up at the same time as the current timetable. This timetable is no longer feasible during line interruptions but forms a good starting point for the genetic algorithm, which now attempts to generate a valid solution. The existing timetable is thus considered the first individual, while all the information within the timetable forms the chromosome and one piece of information represents the gene.

Just as in evolution, a single individual does not form a generation. For this reason the timetable is copied n times, meaning the first population consists of identical timetables, or n individuals.

Each individual (timetable) is then evaluated according to how well it completes the task, i.e. how close it comes to a feasible, valid timetable. The evaluation function relies on the assumption that a bad timetable consists of a lot of conflicts and a good timetable of only a few. If a timetable contains a lot of conflicts, it is assigned a high error value and vice versa. Furthermore, the error function includes an evaluation of delays, which have a smaller weighting. This leads to the secondary condition that a good timetable incurs few delays. Occupancy conflicts have a medium weighting and closed tracks a very high weighting in the error function.

In the first generation, the error value is obviously the same for all individuals, since the first population consists of copies of the initial known timetable. The genetic algorithm follows nature’s pattern and forms the next generation in a process analogous to human reproduction, whereby one individual is chosen at random to be the mother and another to be the father, with individuals with low error values being preferred. These two individuals become parents. The parents’ genes are mixed at random. Mixing the chromosomes produces a descendant (a new individual = a new timetable). The individual undergoes more random mutations, i.e. after the new individual has been generated, and the algorithm is permitted to subject the genes to more random mutations. This makes the new timetable the first child of the new generation, which may differ from its parents due to the mutation.

This process is carried out n times until new generations of timetables are formed. After the new timetables have been evaluated, the reproduction cycle begins again, i.e. the next generation is produced. This process is repeated until an individual solves the problem, i.e. until a timetable is found that sufficiently meets the conditions for a feasible timetable.

Since it must be assumed that the algorithm will not necessarily find the best timetable, we re-start the algorithm several times and present all of the solutions it finds to the timetable planner. They can then select and activate their favourite from the proposed timetables or modify it further according to their own criteria.

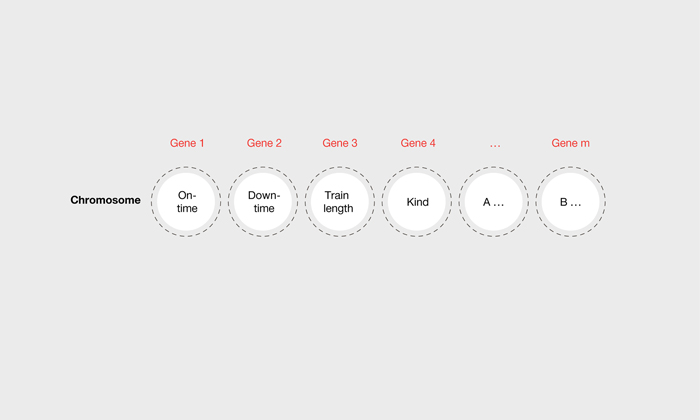
Figure 2: Diagram of a chromosome that represents the timetable, with its characteristics represented as genes

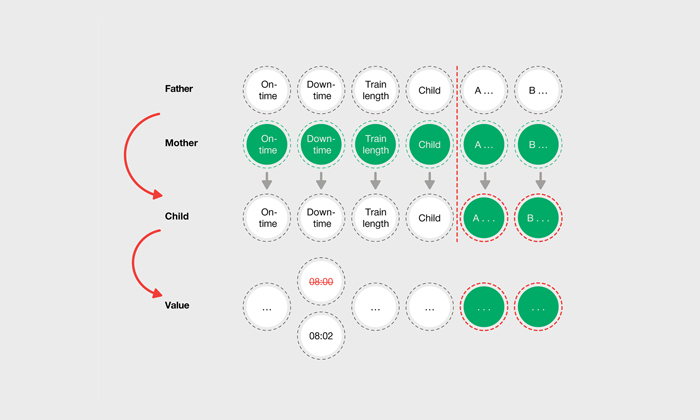
Figure 3: Schematic showing how two chromosomes reproduce

Software developed in-house

The software we describe in this article is a ‘demo’ application. It aims to determine how feasible it would be to automate a precisely defined task – to automatically reschedule an existing timetable – within SBB. The project was carried out using agile methodologies to help us react quickly to the results and integrate the new findings directly into the prototype.

The software currently collects its data from SBB’s own peripheral systems for timetable planning and network topologies. In the next step, the core algorithm is due to be developed further in terms of the software and adapted for use on high performance computing architectures (HPCA). Since the algorithm offers a very high level of parallelisability, the calculation is due to be adapted further to run on the new high-tech platforms. The greatest challenge will be representing the data in such a way that an optimised structure for HPCA can be found.

The aim is to develop an application for optimising a timetable at the push of a button that can be used across Switzerland. The difficulty with this aim is that it involves over 100,000 train journeys and more than 6,000 points, producing an almost infinite problem space (search space). That is why our current aim may sound utopian. The work already carried out on the subject was long considered idealistic by many experts too. Yet a nodal timetable can indeed be generated today at the push of a button.

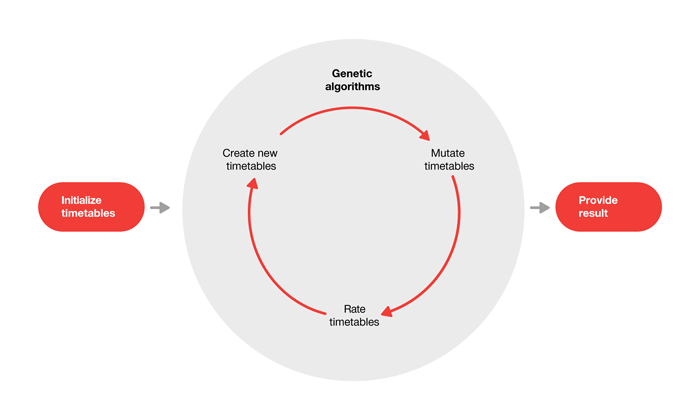
Figure 4: Schematic showing how the genetic algorithm works

Biography

Dirk Abels studied computer science with a special focus on Artificial Intelligence. He is the Head of the ‘Platform of Research and Innovation’ in the Solution Centre for the Infrastructure Division at Swiss Federal Railways (SBB). In this role he is responsible for experimental solutions and looking for unknown answers to questions concerning railway optimisation.

Jürg Balsiger is a certified business information specialist – MBA ‘IIMT’; International Institute of Management in Technology (University of Fribourg). Jürg is Head of Information Technology of the Infrastructure Division at Swiss Federal Railways (SBB). In this role he is responsible for solutions such as the ‘Rail Control System’. Prior to 2010, Jürg was Global Director of Enterprise Infrastructure Architecture at Ernst & Young.