Predicting deterioration in track condition

Trackbed maintenance is a fact of railway life. It is the price the industry pays for utilising loose stones as a track foundation. It is simply uneconomical to use less deformable material – such as concrete – other than for certain high-value lines, notably high-speed routes, and experience in France for example is that high-speed and ballasted track are still quite compatible. It seems likely therefore that the ballasted trackbed will be with us for the foreseeable future, which means that it is essential to do what we can to predict the rate at which it deteriorates and the factors that affect it.

Many of the key elements affecting trackbed performance are obvious enough – although not necessarily fully understood. Ballast quality must, of course, be controlled. Stones must be angular; this allows them to ‘lock up’, making it hard for one stone to slip past another. Ballast must be durable, otherwise stones will readily fragment and the ballast layer will rapidly revert to a dense impermeable and highly weather susceptible material. Foundation quality must not be excessively variable, otherwise problems such as those encountered at transitions between structures and ground-bearing track may occur. There has to be sufficient thickness of material above a soft and deformable subgrade. There has to be a means of preventing intermixing of soft subgrade and coarse granular ballast. All of these are well known and are covered by specifications, primarily written based on many years of experience. But being well known is one thing; are they really understood? Are the measures of ballast quality that are commonly used the correct measures? Do we really know what limits should be placed on foundation non-uniformity? These are the questions that ongoing research at the University of Nottingham is seeking to address.

Understanding the problem

The primary maintenance requirement is to correct track alignment, principally vertical alignment although horizontal ‘drift’ also occurs. Basically, unbound trackbeds suffer from differential settlement leading to uneven ride quality – which is a vicious circle since uneven ride quality leads to increased dynamic force components from train axles and this in turn accelerates the differential settlement.  The problem therefore is not simply settlement but differential settlement, and there is no  real reason to expect any reliable relationship between the two. Naturally, if there is  no settlement then there can be no differential settlement; but whether a settlement limit can be used as a surrogate for a differential settlement limit seems highly doubtful.  The problem can therefore be broken down  into two components:

1. Understand and predict settlement of a single sleeper in response to repeated vertical load
2. Model the interaction of track unevenness and induced dynamic load, leading to uneven load distribution (and therefore differential settlement)

Unless both of these can be achieved then it will be impossible to make any meaningful prediction of trackbed deterioration.

Settlement of a single sleeper

The Nottingham University Railway Test Facility (RTF) (see Figure 1 on page 44) is a full scale  3-sleeper rig with a realistic trackbed construction (ballast overlying soil of controlled properties), which allows realistic loads to be applied and measurements taken of sleeper settlement. Recently, innovative measurement of the movement of individual ballast particles beneath the surface has also been carried out, allowing the pattern of movement to be studied, and the clear message is that the bulk of the deformation occurs within the upper third of the ballast layer, even where a relatively soft subgrade is present.

So much for observation; the problem is how to develop an analysis approach that enables this behaviour to be understood and modelled. And the reason why this is such a difficult task is that railway ballast, like all particulate materials, is immensely complex in the way it reacts to stresses in different directions. In a recent test of a finite element analysis of the problem, which in the end  could only be considered approximate  because of the need to idealise ballast behaviour, it revealed the fact that, perhaps unsurprisingly, ballast beneath a sleeper  really does act like a pile of stones! There was  a clear angle of load spread (perhaps around 15°) which suggested that a simple way  forward would be to assume the load spread effect and to calculate the likely settlement within each of the several sub-layers, using an appropriate equation for strain due to repeated load. Since the load was more concentrated near to the sleeper while the ‘confinement’ was less because of relatively shallow overburden, the inevitable result is that it was the part  of the ballast just beneath the sleeper that suffered most strain, i.e. it was the leading contributor to settlement. Figure 2 on page 45 shows measured and predicted settlements using this approach over a million cycles of load in the RTF, including prediction at different levels within the ballast1.

The clear message is that it is quite possible to predict the settlement of a single sleeper. Ballast properties (notably shear strength) have to be measured (or assumed), but if this can be achieved then a sensible estimate can be made for the way in which settlement increases.

Differential settlement

But of course settlement is not the problem;  it is differential settlement. And differential settlement cannot possibly be measured at full scale in a laboratory. It requires many tens of metres over which a fast-moving train can experience dynamic movement of its suspension system, responding to track unevenness. However, it can be measured on site, and Figure 3 shows the pattern of differential settlement (expressed as track standard deviation) followed by tamping on two different sections of track, both constructed at the same time (1982/3) and to the same nominal specification.

Maintenance engineers will not be surprised to see that there are considerable differences between them; they would be likely to put this down to differences in the underlying subgrade – and they would almost certainly be correct.

The approach taken to this problem at the University of Nottingham has been to use a simple dynamic model of the vertical oscillation of a single carriage end on its suspension system, giving oscillating axle load. The suspension system also has to respond to relative vertical movement of the bogies due to track unevenness. The start condition is  defined by an initial imperfect vertical profile, intended to correspond to the condition immediately after a tamping operation. This profile is applied over 160m of track; rail type, sleeper spacing and trackbed stiffness also have to be defined and this last property can be varied to represent a non-uniform subgrade.  A defined axle load is then ‘run’ along the track at a selected speed with a certain carriage end mass and a defined spring-and-dashpot suspension system. The result is a predicted distribution of load along the track, which can be converted to a predicted set of individual sleeper loads and, using the single sleeper settlement analysis, a settlement rate (millimetres per million axle loads) for each sleeper. After a number of axles have passed, differential settlement will have noticeably changed the track profile, at which point the dynamic analysis has to be rerun and a new set of sleeper loads obtained (see Figure 4 on page 46).

Example output – effect of  train variables

As stated at the beginning of this article, this is a work in progress, particularly the development of improved single sleeper settlement predictions. Nevertheless, provisional results have been obtained as follows.

Axle Weight

The fact that increased axle weight can dramatically affect the rate of track deterioration has become very clear in the UK  in recent years with the adoption of heavier passenger carriages on some train sets. Figure 5 on page 46 illustrates the effect for different goods train axle weights on a particular track structure. The detail may be open to question – the sudden changes apparent in places in  Figure 5 on page 46 are due to the incremental nature of the computation – but the very clear message is that axle weight is critical. More importantly, its influence can be predicted.

Suspension system

Suspension system design is not generally determined by its effect on the track.  Rather it is safety, passenger comfort and the need to avoid impact type forces between components of the train that influence design. Nevertheless, as Figure 6 shows, the effect on the track is real enough. At a given axle weight and train speed, a soft suspension can significantly reduce the development of differential settlement.

Train speed

Figure 7 doesn’t really do this subject justice since it is a complex issue. However, it makes the point that there is no single trend of deterioration rate against speed. In this case, 90mph (about 140kph) gives worse performance than either faster or slower speeds, but the story would be different with different train-track combinations. It is a function of the interaction between the natural frequency of the suspension system and the track deformation wavelengths.

Example output – effect of  track variables

The following predictions all relate to the same train travelling at the same speed.

Subgrade stiffness

Most people would expect this to be a critical parameter, and they would expect a poorer performance over soft subgrade. This analysis however (see Figure 8 on page 48) does not support this view. While soft subgrade may be associated with a range of problems, notably intermixing of ballast and subgrade or deformation within the subgrade itself, it does not cause any particular problems in the upper ballast where most of the settlement is predicted to occur in a well-designed track. In fact, the opposite is true since a stiff support means that the rail bends less and so spreads the load between sleepers less efficiently. Note however that a variable subgrade (within the 80-120MN/m3 range) is just as much of a problem as a stiff but uniform subgrade.

Sleeper spacing

Applying a random variation in sleeper spacing within certain limits (either ±25mm or ±50mm) (see Figure 9) seems to have some impact on differential settlement initially, but the effect disappears after a few hundred thousand load applications. It seems to take time for the pattern of differential settlement to conform itself to the pattern of sleeper spacings. Increasing average spacing from 0.65m to 0.70m on the other hand leads to a dramatic increase in deterioration rate.

Potential findings

The beauty of this sort of simulative analysis is that more or less any variation can be investigated. This short article has concentrated on a few key variables, but the potential exists for much more. It would be possible to play around with the details of train suspension (primary and secondary) for instance. Sleeper mass, width, depth etc. are all predicted at this stage to have a significant influence, although results are not presented here because it is considered that there is a need to check these predictions out experimentally first. Similarly, ballast properties are predicted to be highly significant, and the key parameters (principally angle of internal friction) are not those directly specified at present.

One could go further and look at issues such as the inclusion of an elastic ‘boot’ at the base of the sleeper, something which has been tried but which is not understood sufficiently to be sure whether it is economically justifiable or not. Predictive analysis has the power to evaluate such ideas without having to wait years for data.

Conclusion

A railway track is a magnificent structure whose design is based principally on decades of experience. Yet reliance on experience can be as much of a hindrance as a help. It means that it is difficult to accept changes. The resulting culture is that nothing can be trusted until proven in practice; but then on what basis can one decide what to trial? Without an accelerated predictive approach the danger is that either nothing new is ever tried or else vast sums of money are wasted on economically unjustifiable ideas. This article is a plea for the adoption of an improved scientific basis for trackbed design.

Reference

1. Work carried out by research student  Xiaoyi Shi

Figure 1: Full scale 3-sleeper rig witha realistic trackbed construction

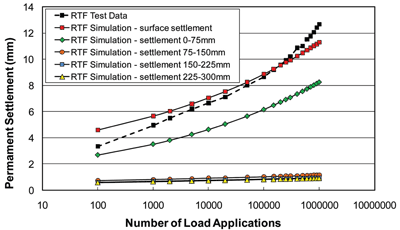
Figure 2: Measured and predicted settlement in the Railway Test Facility

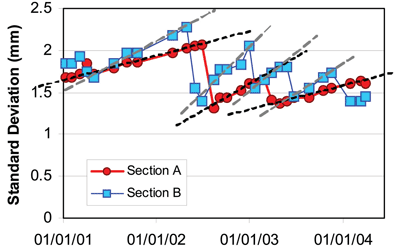
Figure 3: Track recording car data - East Coast Main Line

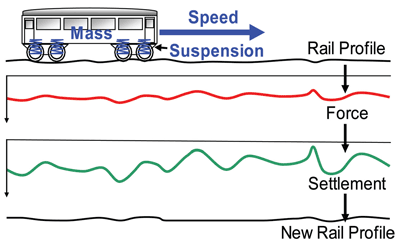
Figure 4: Dynamic analysis procedure

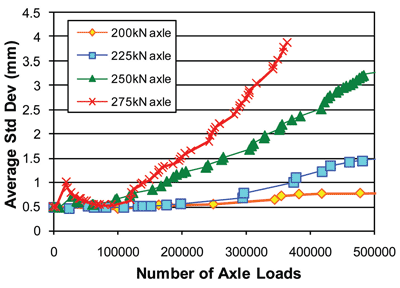
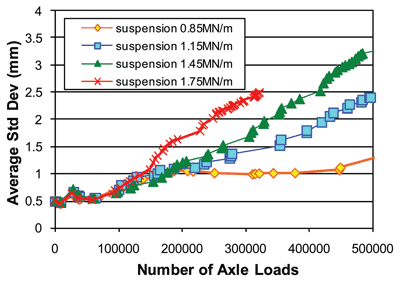
Figure 6: The effect of suspension stiffness

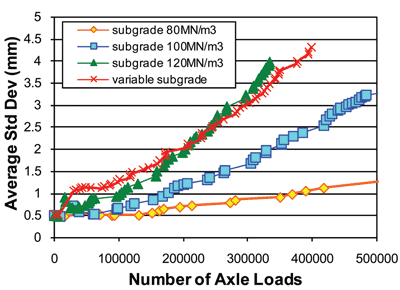
Figure 8: The effect of subgrade stiffness

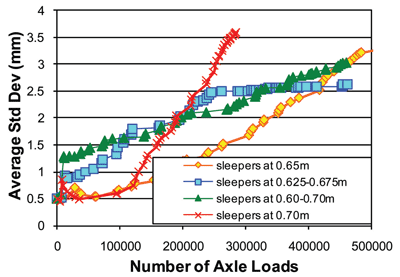
Figure 9: The effect of sleeper spacing